Memorandum
PART A: Dynamic Responses of Two Real Systems
1. Dynamics of a U-Tube Manometer
The U-tube manometer response to the time-varying pressure differential was investigated for different types of liquids and tube diameters. The first tube is a large diameter water manometer. The second tube is a mixture of glycerine and water manometer with the same diameter as the first one and the last tube is a small diameter water manometer. In the first U-tube manometer, water oscillated for about10 time before the it returned to the initial level (damped out). In the glycerine/water manometer, it only took about one oscillation before the liquid mixture damped out. In the last manometer, it took about 4 oscillations before the water damped out. The reason for this dynamic behaviors can be best explained in term of damping coefficient, z, which was found to be proportional to liquid viscosity, m, but inversely proportional to the square of the tube radius, R2, (see sample calculations). Low values of z imply a more oscillatory response. So, it is not surprising that water in the first U-tube oscillated more than the water in the third tube and the glycerine/water mixture in the second tube.
2. Dynamic Response of Three Stirred Vessels in Series
Figure 1 shows the response of three stirred vessels to the salt solution (rectangular) pulse. As expected, the fastest response (salt conductivity) was seen in Tank 1, followed by Tank 2 and then Tank 3. After a few minutes, the input was switched from salt solution to DI water. The results were also expected. The response in Tank 1 quickly decreased in time, followed by those in Tank 2 and lastly in Tank 3. The reason for this behavior is simple. When the salt solution entered the first tank, the conductivity (response) in the tank increased. The same thing happens in second tank after the entrance of the salt solution from Tank 1. Finally, the salt solution from Tank 2 entered the third tank and the conductivity in that tank increased. The explanation to the decrease of the responses is just the reverse of that above.
The general form of transfer function for the three vessels in series are:
![]() Tank 1
Tank 1
![]() or
or ![]() Tank 2
Tank 2
![]() or
or ![]() Tank 3
Tank 3
PART B: Simulation of 2nd and 3rd Systems with Program CC
1. U-Tube Manometer Dynamics
The general form of the dynamics of manometer deflection (H) was found to be:
![]()
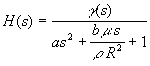
Note: please see the nomenclature in Sample Calculations.
In Figure 2, manometer deflection (response) was plotted at different radii (R = 0.05, 0.15 and 0.30 cm). As explained in Part A.1, the response is inversely proportional to R2. The smaller the radius, the less oscillatory the response is. This explain why the curve of the response to the smallest diameter (R = 0.05 cm) was overdamped, the one for the middle diameter (R = 0.15 cm) was critically damped and the one for the biggest diameter (R = 0.30 cm) was underdamped. As a general guideline, the response will be oscillatory if the value of m/r is in between 0 and 2R2a0.5/b as found in the Sample Calculations.
The response of the manometer to different liquid viscosities (m = 0.01 for water and 0.1 g/cm.s for the polymer solution) was plotted in Figure 3. Higher viscosity implies an overdamped response while the lower viscosity means that the response will be more oscillatory.
The manometer response to the sinusoidal forcing function was also investigated. The forcing function, g2(t), was plotted in the same graph with the response. From Figure 4, the phase lag, f, was found to be 1.93rad and the amplitude ratio, AR, was determined to be 0.83. As a comparison to the theoretical values, f and AR was also calculated from equations (5-61) and (5-63), respectively and found to be 1.12rad and 0.83. While the AR found from the plot agrees with the theoretical one, the f values do not. The reason for the difference is probably that the f from the plot was calculated at time less than 10 sec while that from the equation was derived at larger value of time. The f values will agree if the time axis is extent so that the more steady oscillation can be obtained.
2. Three CSTRs in Series
From Figure 5, in general, the responses to the rectangular pulse are similar to those obtained experimentally (Part A.1). In both Figures 1 and 5, the response in Tank 1 was the first to peak and also the first to decrease. The one in Tank 2 was the next to peak and slowly decreased after some time. However response in Tank 2 remained above the conductivity value of the solution in Tank 1 after it tailed off. The response in Tank 3 was the slowest to increase and also to decrease although it ended up at the highest conductivity value after some time.
PART B
1.c) Using ZEROS in Program CC, the roots (s) were found:
ForR = 0.05 cm, s1 = 0.0, s2 = -0.52 and s3 = -31.5
R = 0.15 cm, s1 = 0.0, s2 = -1.78 + 3.63j, s3 = -1.78 - 3.63j
R = 0.30 cm, s1 = 0.0, s2 = -0.44 + 4.02j, s3 = -0.44 - 4.02j
where j = (-1)1/2